Un espacio euclídeo de dimensión finita es un espacio vectorial normado sobre los números reales de dimensión finita, en que la norma es la asociada al producto escalarordinario. Para cada número entero no negativo n, el espacio euclídeo n-dimensional se representa por el símbolo  y es el conjunto de todas las tuplas ordenadas
y es el conjunto de todas las tuplas ordenadas
 y es el conjunto de todas las tuplas ordenadas
y es el conjunto de todas las tuplas ordenadas
en donde cada  es un número real, junto con la función distancia entre dos puntos (x1, ..., xn) e (y1, ..., yn) definida por la fórmula:
es un número real, junto con la función distancia entre dos puntos (x1, ..., xn) e (y1, ..., yn) definida por la fórmula:
 es un número real, junto con la función distancia entre dos puntos (x1, ..., xn) e (y1, ..., yn) definida por la fórmula:
es un número real, junto con la función distancia entre dos puntos (x1, ..., xn) e (y1, ..., yn) definida por la fórmula:
Esta función distancia es una generalización del teorema de Pitágoras y se denomina distancia euclidiana. El hecho de que se haya definido una distancia permite definir otros conceptos métricos como el de medida de Lebesgue (lo cual permite a su vez definir la longitud de una curva (1-volumen), las nociones de área (2-volumen), volumen (3-volumen) y cuando el espacio tiene dimensión superior a 3 n-volumen (para n > 3).
Además pueden definirse ángulos, al poder hablar de proyectar una longitud recta sobre la dirección de otra longitud recta no paralela, así el ángulo entre dos rectas r1 y r2cuyos vectores unitarios tangentes son 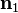 y
y 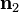 se puede definir como:
se puede definir como:
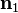 y
y 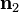 se puede definir como:
se puede definir como:Bibliografia:
https://es.wikipedia.org/wiki/Espacio_eucl%C3%ADdeo

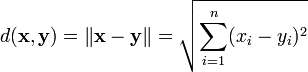

No hay comentarios:
Publicar un comentario